1. 진법과 진법 변환
1) 디지털 정보의 단위
bit -8- byte -4- nibble
- 1문자당 영어는 1byte, 한글은 2bytes(16비트) 필요
- 워드 : 특정 CPU에서 취급하는 명령어나 데이터의 길이에 해당하는 비트수. 8비트 배수 가능
킬로 메가 기가 테라 페타 엑사 제타 요타
키비 메비 기비 테비 페비 엑비 제비 요비
10의 3승씩 증가
2의 10승씩 증가
2) 진법
- 10진법 2진법 8진법(한자리=2진수 세자리) 16진법
- 10진수와 나머지는 곱과 나누기를 이용해 변환. 2,8,16끼리는 2진수를 바꾼 다음 변환
이진수 1100 1110 1001 1010 → 12 14 9 10 → C E 9 A
이진수로 바꾼뒤 / 자리수대로 다시 잘라서 십진수로 표현하고 / 십진수에 해당하는 n진수기호 넣기
** 16진수는 0~9, A10~D13~F15
** 자리수대로 다시 자를 때 정수부앞과 소수부뒤에 자리수가 안맞으면 빈자리 0으로 채움!!
(62)_8 = (110 010)_2 = (0011 0010)_2 → 10진수로 각 3, 2임. 3, 2는 16진수로도 3, 2→ (32)_16
소수를 포함한 진법 변환
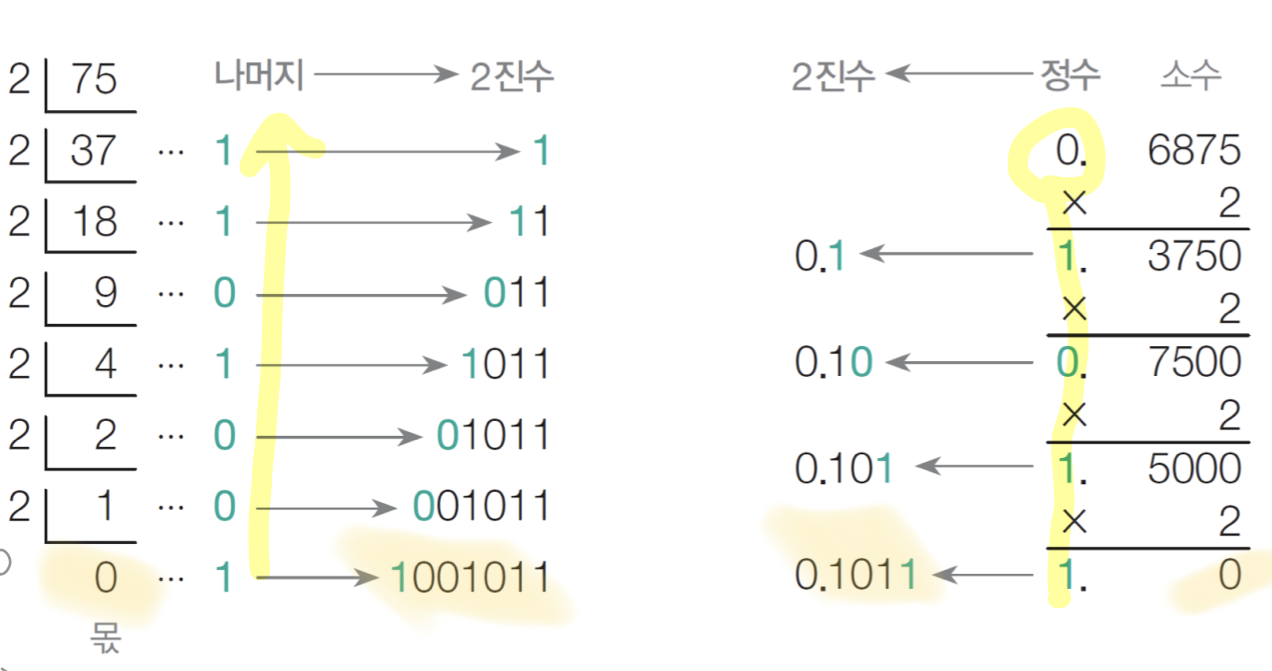
- 10진수 → 2진수 : 정수는 2나누기, 소수는 2곱하기해서 .밖 수를 계속 분리함
- 10진수 → 8진수 : 8로함
- 16진수도. 대신 16진수는 숫자가 두자릿수도 나오는데 그건 A~F로 바꿔서!
- 아니면 그냥 다 2진수로 바꾸고 2진수를 다른걸로 바꿔도 됨
2. 정수표현
1) 보수의 개념과 음수
- 정수 ⇒ MSB는 부호비트임!!!!!
- r진법은 두 가지의 보수가 존재함. r-1의 보수 → r의 보수
- r-1의 보수를 구하고 +1하면 r의 보수가 됨
- 컴퓨터에서는 2진수로 정수를 표현한다.
- 2진법에서 음수는 양수의 2의 보수로 표현함. (양수는 그대로 표현하면 2의 보수로 표현과 같음)
- 구하는 순서 : 1의보수 → 2의 보수
- 2진법에서 1의 보수를 구하는 법 = 0은 1로, 1은 0으로 바꾼다.
- 최상위비트만 1인 수는 양수일까 음수일까? → 음수로 침! 0아님!! 0은 다 0임ex) 4비트에서 1000 → -1하면 0111 → 1의보수구하면 1000 = -8로 침
- 8비트 표현범위 : -128~127
- 2의보수를 구하면 원래수와 같은 값이 나옴. 그래서 항상 표현할 수 있는 음수가 양수보다 하나 더 많음
- 다 0인 수는 0임.
** 2진수와 그 수의 1의 보수의 합은 1 (양음관계인데 음수에 +1안한거니까)
2진수롸 그 수의 2의 보수의 합음 0 (양음관계니까)
2) 부호확장
양수는 0, 음수는 1로 채움.
3) 2진 정수 연산
- 뺄셈 = 2의보수(음수)로 바꾼 후 덧셈함!
- 직전캐리 =/= 최종 캐리 이면 overflow!
- overflow는 부화확장으로 해결가능.
4) 10진 정수 표현
십진수로 바로 변환 가능한 이진화 십진법(BCD)
- 팩 10진 형식 packed BCD
- 4비트 당 한 자리수를 표현. 최하위 4비트는 부호를 의미하는 값 넣음(+ C1100, - D1101, 부호없음 F1111)
3. 실수표현
컴퓨터에서의 실수 표현. IEEE 754 표준
- 부동소수점(소수점이 고정되지 않고 소수점의 위치를 나타내는 값을 표기함)
- 단정도 부동소수점수 : 부호비트+지수부8비트+가수부23비트, 바이어스 127 **우린 이거~
- 배정도 부동소수점수
- 계산법
2진수로 바꾸고 → 소수점이 제일 앞1 직전까지 가려면 몇 칸 옮겨야 하는지 세고 → 옮기고 1.생략 후 0채워서 23자리로 만들어 가수부를 구함 → 옮긴 만큼 2의 몇승으로 표현, **+127!!!!!**해서 가수부를 구함
부동소수점수 : ±1.M x 2^E
비트 : 부호 + E!!!! + M
E는 8자리, M은 23자리
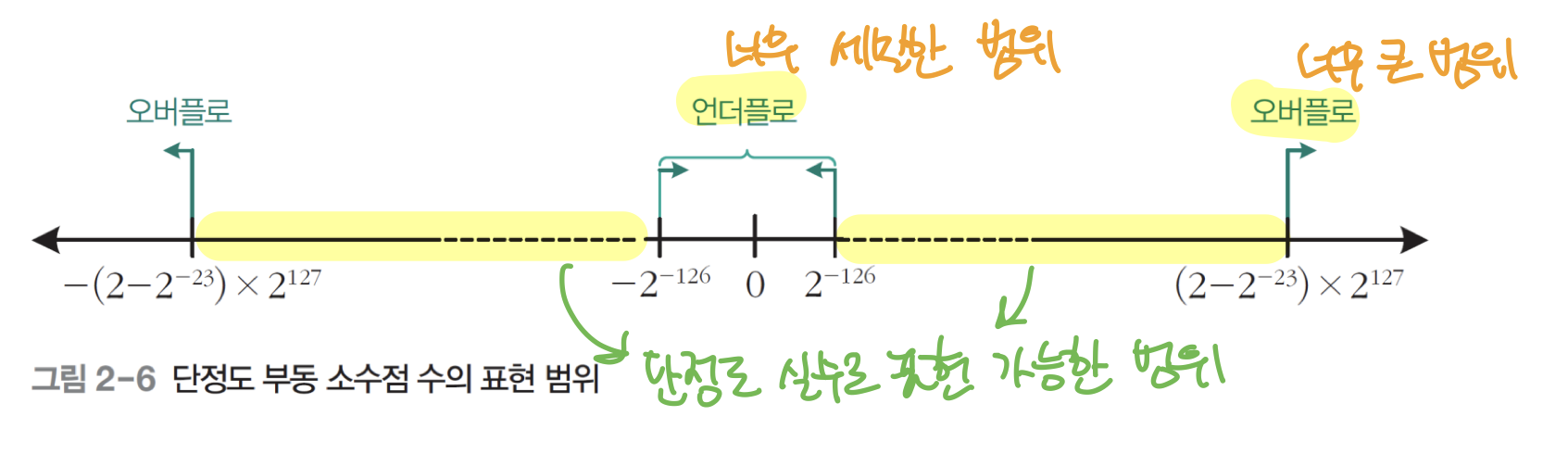
- 컴퓨터에서의 부동소수점 표현 범위
4. 디지털 코드
1) BCD코드(8421코드)
- 10진수 한자리를 4비트로 표현해 연결
- 0~9를 2진화. 표기는 2진이지만 의미는 10진.
BCD코드 0001 0101 = 10진수 15
이건 계산문제 안내요 원리만..
2) 3초과 코드 : BCD +3
0↔9, 4↔5 등 자기보수의 성질이 있음! 서로 0 1 뒤집으면 똑같음
3) 그레이 코드 : 연속수는 한비트만 변경
1 = 0001
2 = 0011
3 = 0010
4 = 0110
4) 다양한 2진코드 : 가중치, 비가중치 코드
- 가중치 코드
- 2421코드 : 4비트의 각 자리수 가중치가 2421임. 자보수 성질.
- 비가중치 코드
- 자리수에 따른 가중치 없음. 3초과코드, 그레이 코드.
5) 영숫자(alphanumeric) 코드
- ASCII코드
- 유니코드 : ASCII코드 한계극복
- 한글 완성형, 조합형 (조합형 한글자에 2바이트=16비트)
5. 에러 검출 코드
1) 패리티 비트
- 짝/홀수패리티 : 1의 개수를 짝/홀수개로 맞춤
- 에러검사를 위해 앞에 한비트씩 추가비트
- 에러 검출만 가능!! 여러비트 에러 시 검출 안될 수도(근데 잘 안남).
2) 해밍코드
- 어느자리에 오류났는지까지 가능! 에러 정정 가능
- 짝수패리티
- 데이터가 d비트짜리이면 아래 식을 만족하는 p개의 패리티비트 필요.
- 2^p ≥ p+d+1
- 패리티 비트p_n은 데이터 사이사이 2의 승자리에 들어감.어감.
'뚝딱 공부 상자 > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] Chapter6. 기억장치 (0) | 2022.06.25 |
|---|---|
| [컴퓨터 구조] Chapter5. 제어 장치 (0) | 2022.06.25 |
| [컴퓨터 구조] Chapter 04. 중앙 처리 장치 (0) | 2022.06.25 |
| [컴퓨터 구조] Chapter 03. 디지털 논리 회로 (0) | 2022.06.25 |
| [컴퓨터 구조] Chapter 01. 서론 (0) | 2022.06.25 |
1. 진법과 진법 변환
1) 디지털 정보의 단위
bit -8- byte -4- nibble
- 1문자당 영어는 1byte, 한글은 2bytes(16비트) 필요
- 워드 : 특정 CPU에서 취급하는 명령어나 데이터의 길이에 해당하는 비트수. 8비트 배수 가능
킬로 메가 기가 테라 페타 엑사 제타 요타
키비 메비 기비 테비 페비 엑비 제비 요비
10의 3승씩 증가
2의 10승씩 증가
2) 진법
- 10진법 2진법 8진법(한자리=2진수 세자리) 16진법
- 10진수와 나머지는 곱과 나누기를 이용해 변환. 2,8,16끼리는 2진수를 바꾼 다음 변환
이진수 1100 1110 1001 1010 → 12 14 9 10 → C E 9 A
이진수로 바꾼뒤 / 자리수대로 다시 잘라서 십진수로 표현하고 / 십진수에 해당하는 n진수기호 넣기
** 16진수는 0~9, A10~D13~F15
** 자리수대로 다시 자를 때 정수부앞과 소수부뒤에 자리수가 안맞으면 빈자리 0으로 채움!!
(62)_8 = (110 010)_2 = (0011 0010)_2 → 10진수로 각 3, 2임. 3, 2는 16진수로도 3, 2→ (32)_16
소수를 포함한 진법 변환
- 10진수 → 2진수 : 정수는 2나누기, 소수는 2곱하기해서 .밖 수를 계속 분리함
- 10진수 → 8진수 : 8로함
- 16진수도. 대신 16진수는 숫자가 두자릿수도 나오는데 그건 A~F로 바꿔서!
- 아니면 그냥 다 2진수로 바꾸고 2진수를 다른걸로 바꿔도 됨

2. 정수표현
1) 보수의 개념과 음수
- 정수 ⇒ MSB는 부호비트임!!!!!
- r진법은 두 가지의 보수가 존재함. r-1의 보수 → r의 보수
- r-1의 보수를 구하고 +1하면 r의 보수가 됨
- 컴퓨터에서는 2진수로 정수를 표현한다.
- 2진법에서 음수는 양수의 2의 보수로 표현함. (양수는 그대로 표현하면 2의 보수로 표현과 같음)
- 구하는 순서 : 1의보수 → 2의 보수
- 2진법에서 1의 보수를 구하는 법 = 0은 1로, 1은 0으로 바꾼다.
- 최상위비트만 1인 수는 양수일까 음수일까? → 음수로 침! 0아님!! 0은 다 0임ex) 4비트에서 1000 → -1하면 0111 → 1의보수구하면 1000 = -8로 침
- 8비트 표현범위 : -128~127
- 2의보수를 구하면 원래수와 같은 값이 나옴. 그래서 항상 표현할 수 있는 음수가 양수보다 하나 더 많음
- 다 0인 수는 0임.
** 2진수와 그 수의 1의 보수의 합은 1 (양음관계인데 음수에 +1안한거니까)
2진수롸 그 수의 2의 보수의 합음 0 (양음관계니까)
2) 부호확장
양수는 0, 음수는 1로 채움.
3) 2진 정수 연산
- 뺄셈 = 2의보수(음수)로 바꾼 후 덧셈함!
- 직전캐리 =/= 최종 캐리 이면 overflow!
- overflow는 부화확장으로 해결가능.
4) 10진 정수 표현
십진수로 바로 변환 가능한 이진화 십진법(BCD)
- 팩 10진 형식 packed BCD
- 4비트 당 한 자리수를 표현. 최하위 4비트는 부호를 의미하는 값 넣음(+ C1100, - D1101, 부호없음 F1111)
3. 실수표현
컴퓨터에서의 실수 표현. IEEE 754 표준
- 부동소수점(소수점이 고정되지 않고 소수점의 위치를 나타내는 값을 표기함)
- 단정도 부동소수점수 : 부호비트+지수부8비트+가수부23비트, 바이어스 127 **우린 이거~
- 배정도 부동소수점수
- 계산법
2진수로 바꾸고 → 소수점이 제일 앞1 직전까지 가려면 몇 칸 옮겨야 하는지 세고 → 옮기고 1.생략 후 0채워서 23자리로 만들어 가수부를 구함 → 옮긴 만큼 2의 몇승으로 표현, **+127!!!!!**해서 가수부를 구함
부동소수점수 : ±1.M x 2^E
비트 : 부호 + E!!!! + M
E는 8자리, M은 23자리
- 컴퓨터에서의 부동소수점 표현 범위

4. 디지털 코드
1) BCD코드(8421코드)
- 10진수 한자리를 4비트로 표현해 연결
- 0~9를 2진화. 표기는 2진이지만 의미는 10진.
BCD코드 0001 0101 = 10진수 15
이건 계산문제 안내요 원리만..
2) 3초과 코드 : BCD +3
0↔9, 4↔5 등 자기보수의 성질이 있음! 서로 0 1 뒤집으면 똑같음
3) 그레이 코드 : 연속수는 한비트만 변경
1 = 0001
2 = 0011
3 = 0010
4 = 0110
4) 다양한 2진코드 : 가중치, 비가중치 코드
- 가중치 코드
- 2421코드 : 4비트의 각 자리수 가중치가 2421임. 자보수 성질.
- 비가중치 코드
- 자리수에 따른 가중치 없음. 3초과코드, 그레이 코드.
5) 영숫자(alphanumeric) 코드
- ASCII코드
- 유니코드 : ASCII코드 한계극복
- 한글 완성형, 조합형 (조합형 한글자에 2바이트=16비트)
5. 에러 검출 코드
1) 패리티 비트
- 짝/홀수패리티 : 1의 개수를 짝/홀수개로 맞춤
- 에러검사를 위해 앞에 한비트씩 추가비트
- 에러 검출만 가능!! 여러비트 에러 시 검출 안될 수도(근데 잘 안남).
2) 해밍코드
- 어느자리에 오류났는지까지 가능! 에러 정정 가능
- 짝수패리티
- 데이터가 d비트짜리이면 아래 식을 만족하는 p개의 패리티비트 필요.
- 2^p ≥ p+d+1
- 패리티 비트p_n은 데이터 사이사이 2의 승자리에 들어감.어감.
'뚝딱 공부 상자 > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] Chapter6. 기억장치 (0) | 2022.06.25 |
|---|---|
| [컴퓨터 구조] Chapter5. 제어 장치 (0) | 2022.06.25 |
| [컴퓨터 구조] Chapter 04. 중앙 처리 장치 (0) | 2022.06.25 |
| [컴퓨터 구조] Chapter 03. 디지털 논리 회로 (0) | 2022.06.25 |
| [컴퓨터 구조] Chapter 01. 서론 (0) | 2022.06.25 |
